Context
Last week, I was discussing about how to use nls() for a specific
model with one of my colleague and I ended creating a piece of code to
show what I was talking about! Even though there are many posts exploring nls()
in more depth that I did (for instance this post on datascienceplus by Lionel Herzog),
I thought I could share these lines of command here!
Basically, we were talking about a model where the temperature ($T$) follows
a saturation curve starting from 10°C at t=0 (so T(0) = 10) and plateauing at \(T_{\inf}\).
$$T(t) = T_{\inf} - (T_{\inf} - T_0)\exp(-kt)$$
Goal and data
The goal here is to use nls() (Nonlinear Least Squares) to find \(k\) and \(T_{inf}\).
For the sack of clarity, I simulate the data, i.e. I use the saturation curve
with known parameter values, then I add some noise (here a white noise):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
library(magrittr)
# Parameters
## known
T0 = 10
## the ones we are looking for
k = 0.2
Tinf = 20
# Simulate data
## time
seqt <- seq(0, 50, .25)
## create a data frame
simdata <- cbind(
seqt = seqt,
sim = Tinf - (Tinf- T0) * exp(-k * seqt) + .5 * rnorm(length(seqt))
) %>% as.data.frame
head(simdata)
#R> seqt sim
#R> 1 0.00 9.366208
#R> 2 0.25 10.724386
#R> 3 0.50 11.112208
#R> 4 0.75 10.677729
#R> 5 1.00 11.376080
#R> 6 1.25 12.713639
|
Use nls()
Now I call nls() to fit the data:
1
|
res <- nls(sim ~ Tinf - (Tinf - 10)*exp(-k*seqt), simdata, list(Tinf = 1, k = .1))
|
All the information needed are stored in res and display via the print method:
1
2
3
4
5
6
7
8
9
10
|
res
#R> Nonlinear regression model
#R> model: sim ~ Tinf - (Tinf - 10) * exp(-k * seqt)
#R> data: simdata
#R> Tinf k
#R> 20.0033 0.1951
#R> residual sum-of-squares: 53.84
#R>
#R> Number of iterations to convergence: 8
#R> Achieved convergence tolerance: 1.312e-06
|
Let’s draw a quick plot:
1
2
3
4
5
|
## get the coefficients values
cr <- coef(res)
fitC <- function(x) cr[1] - (cr[1] - 10)*exp(-cr[2]*x)
plot(simdata[,1], simdata[,2], xlab = "Time (min)", ylab = "Temperature (°C)")
curve(fitC, 0, 50, add = TRUE, col = "#2f85a4", lwd = 3)
|
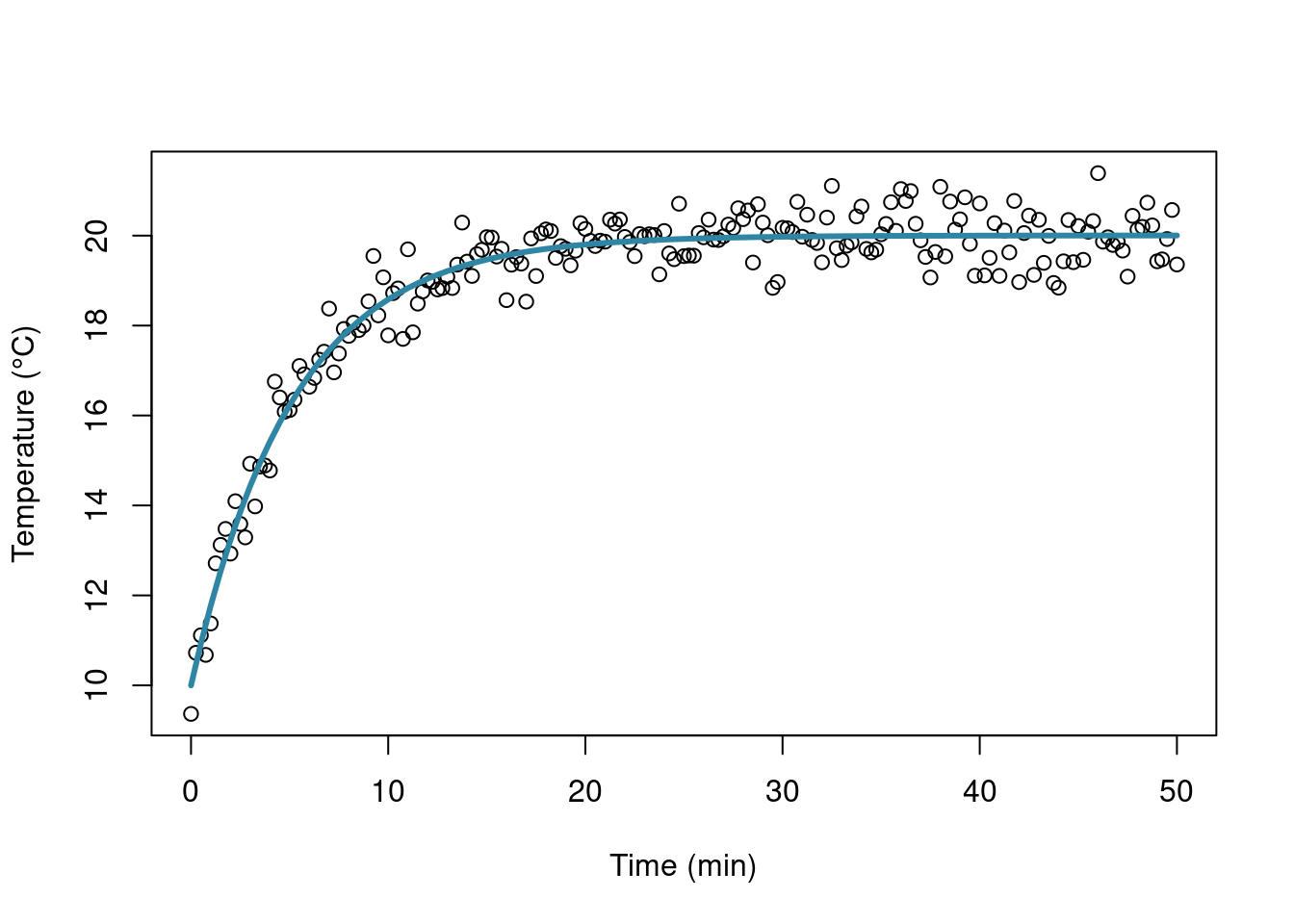
That’s all folks!
Display information relative to the R session used to render this post.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
sessionInfo()
#R> R version 4.3.3 (2024-02-29)
#R> Platform: x86_64-pc-linux-gnu (64-bit)
#R> Running under: Ubuntu 22.04.4 LTS
#R>
#R> Matrix products: default
#R> BLAS: /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3
#R> LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.20.so; LAPACK version 3.10.0
#R>
#R> locale:
#R> [1] LC_CTYPE=C.UTF-8 LC_NUMERIC=C LC_TIME=C.UTF-8 LC_COLLATE=C.UTF-8
#R> [5] LC_MONETARY=C.UTF-8 LC_MESSAGES=C.UTF-8 LC_PAPER=C.UTF-8 LC_NAME=C
#R> [9] LC_ADDRESS=C LC_TELEPHONE=C LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C
#R>
#R> time zone: UTC
#R> tzcode source: system (glibc)
#R>
#R> attached base packages:
#R> [1] stats graphics grDevices utils datasets methods base
#R>
#R> other attached packages:
#R> [1] magrittr_2.0.3 inSilecoRef_0.1.1
#R>
#R> loaded via a namespace (and not attached):
#R> [1] sass_0.4.9 utf8_1.2.4 generics_0.1.3 xml2_1.3.6 blogdown_1.19
#R> [6] stringi_1.8.3 httpcode_0.3.0 digest_0.6.35 evaluate_0.23 bookdown_0.38
#R> [11] fastmap_1.1.1 plyr_1.8.9 jsonlite_1.8.8 backports_1.4.1 crul_1.4.2
#R> [16] promises_1.3.0 fansi_1.0.6 jquerylib_0.1.4 bibtex_0.5.1 cli_3.6.2
#R> [21] shiny_1.8.1.1 rlang_1.1.3 cachem_1.0.8 yaml_2.3.8 tools_4.3.3
#R> [26] dplyr_1.1.4 httpuv_1.6.15 DT_0.33 rcrossref_1.2.0 curl_5.2.1
#R> [31] vctrs_0.6.5 R6_2.5.1 mime_0.12 lifecycle_1.0.4 stringr_1.5.1
#R> [36] fs_1.6.3 htmlwidgets_1.6.4 miniUI_0.1.1.1 pkgconfig_2.0.3 bslib_0.7.0
#R> [41] pillar_1.9.0 later_1.3.2 glue_1.7.0 Rcpp_1.0.12 highr_0.10
#R> [46] xfun_0.43 tibble_3.2.1 tidyselect_1.2.1 knitr_1.46 xtable_1.8-4
#R> [51] htmltools_0.5.8.1 rmarkdown_2.26 compiler_4.3.3
|





